Figure 1.
SCEWL - Sharing Coins Effectively with Ladders
For purposes of this document, a coinpool is defined as an N-of-N multisig bitcoin address where N>2, in which N users each deposit Q sats in such a manner that each user can unilaterally withdraw Q sats from the multisig.
A payment channel is defined as an N-of-N multisig bitcoin address where N=2, in which at least one user deposits Q sats, and a series of one or more “states” allows the users to consensually modify how much they can each unilaterally withdraw from the channel.
Suppose a bitcoin user – whom I shall call Reginald – runs a bitcoin lightning node, and wants to allow groups of up to ~100 people to enter coinpools which Reginald serves in the following manner.
The members of any coinpool served by Reginald each get a payment channel (of a construction to be described in section 13) where they have a key and Reginald has a key. They can use these payment channels to send asynchronous payments for free to one another or to members of any other coinpool run by Reginald.
Each member of a coinpool can exit their coinpool with all of their money at any time (assuming they can pay the requisite mining fees), and they can also use Reginald’s node as a bridge to atomically send money to users of the lightning network, or to users of bitcoin’s base layer, as long as they are willing to pay a “bridge fee” determined by Reginald every time a user wants to use the bridge (he may change the bridge fee each time because mining fees and lightning routing fees change constantly, and he uses the bridge fee to compensate himself for the cost of paying those fees).
Each of Reginald’s coinpools exists independently from all of the others and may continue to exist and operate for an indefinite period of time, that is, until all of its users exit. If Reginald’s node goes down or he decides to stop serving a coinpool, he may do so at any time, whereupon the only things the members of that pool can really do are, exit unilaterally, or wait for Reginald to start serving them again.
Supposing Reginald wants to do this, this goal can be accomplished in the following manner.
Suppose three bitcoin users – whom I shall call Alice, Bob, and Carol – all decide they want to be in a coinpool served by Reginald. They contact Reginald and ask him to set one up. Each user (including Reginald) makes up a keypair whose public key they share with one another. The coinpool will be a multisig consisting of each user’s public key. The bitcoin script looks like this:
It’s also possible to use the Frost keysharding scheme so that there is only one key, making the multisig look like a singlesig. But in this document I assume the construction uses “regular” multisig, because I find it easier to think about.
As mentioned in section 1, each user (Alice, Bob, and Carol) will get a payment channel “inside” the coinpool, and in this channel, the user will have a key and Reginald will have a key. The channel is to be described further in section 13, but for right now, it is enough to describe the payment channel’s initial state: all of the money in the channel will be on Reginald’s side, such that the user has maximum inbound capacity. Consequently, if any user exits the multisig in their initial state, those sats will go into a channel where Reginald controls all of the money.
In a few moments, the users and Reginald will do a “signing ceremony” which will ensure that each user can only withdraw sats from the multisig by putting it into their payment channel. Since the initial states of these payment channels give Reginald full control of those sats, and since the users can only withdraw the money from the multisig into these payment channels, Reginald will start off with full control of all of the money in the multisig.
Because the coinpool will start its life in a state where Reginald has full control of all its funds, the only fair way to fund it is for Reginald to be the sole contributor to the multisig. His money should be the only money going in, otherwise he will get custody of other people's money. Reginald will fund the multisig in such a way that each user’s channel gets an equal-sized amount, which will serve as inbound capacity for that user.
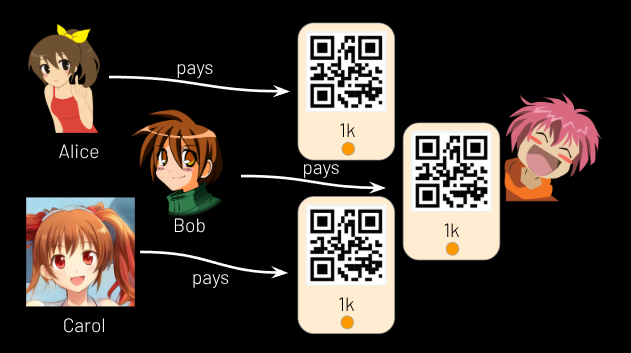
But for now, Reginald simply uses the lightning network to charge each user an initial fee to provide them with this amount of inbound capacity. (See Figure 1.) As a result, each user’s “deposit cost” will be something like 1,000 sats, and this will acquire for them something like 100,000 sats of inbound capacity in their channel. Those two amounts (1,000 and 100,000) are variable and Reginald can adjust them to fit market conditions, but in the rest of this document, I will use them as examples.

Figure 1.
It is possible to make the deposit cost atomic, such that the user’s lightning wallet only sends the 1,000 sats if the user receives a channel in the coinpool worth 100,000 sats. But the only way I know how to do that is to set up a submarine swap, which requires a base layer transaction, and in many cases that will push the cost of atomicity above 1,000 sats. Consequently, it may not make sense for users to do this atomically. If it’s non-atomic, the worst that can happen to each user is that Reginald steals their 1,000 sats, whereas doing it atomically – so that he cannot steal – will probably cost each user more than that. But this depends on how much Reginald charges; if he charges a lot, it may be worth it to the users to set up their deposit in an atomic way, so that he cannot steal it.
At this point, the users pay the deposit cost. This cost also encourages them to continue through the signing ceremony; any user who backs out now loses the deposit cost and accrues no benefit. Unless the payment is done atomically, in which case, some other method should be used to prevent trolling.
Although the users have now paid their deposit cost, Reginald does not yet fund the multisig. First, the users have to do the signing ceremony. The signing ceremony is a period of time during which each user must sign a series of bitcoin transactions, which, together, allow each user to take 100,000 sats out of the multisig and put it into their channel. If any user refuses to sign these, Reginald keeps that person’s money (unless the payment was done atomically) and refunds the others, whereupon the other folks can try again without the offender. (See Figure 2.)
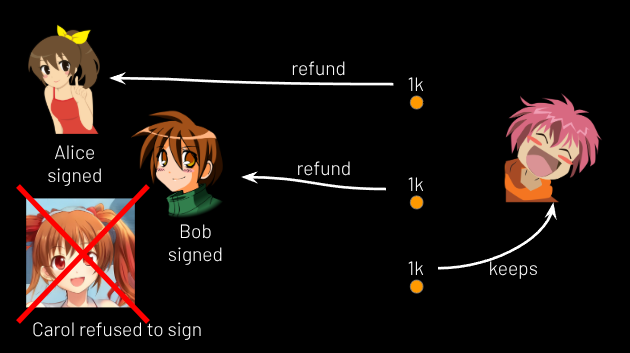
Figure 2.
By having each user of an N-of-N multisig sign this series of transactions, each user, including Reginald, knows that they can get the money into a channel where they have a key, and once it is in such a channel, the channel logic (to be described in section 13) allows that user (and Reginald) to withdraw their “share” of the channel and get it into an address on bitcoin’s base layer.
The signing ceremony depends on each user knowing what utxo will fund the multisig. So at this point, Reginald tells each user what utxo he will use to do that. It must be a utxo worth at least 300,000 sats, so that each user (Alice, Bob, and Carol) gets 100,000 sats in the multisig, which they can withdraw into their channel.
However, it is actually that plus a bit extra, because Reginald’s funding utxo also has to have enough money to give each user a connector output and two anchor outputs. The meaning and function of these outputs will be described in section 6, concerning the exit ladder. For now, it is enough to say that the connector outputs will each be worth 294 sats (the dust limit for segwit v0 addresses) and the anchor outputs will each be worth 240 sats (the dust limit for anchor addresses), so, in our case, where there are 3 users, Reginald’s funding utxo must be worth at least 302,322 sats:
( 100,000 * N ) + ( 294 * N ) + ( 240 * 2N )Here it is in latex format because that’s what whitepapers do:
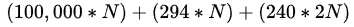
The exit ladder is a new construction that allows for unilateral exit from a coinpool. The exit ladder has the following properties:
To make the exit ladder work, we start by having the users of the coinpool generate and sign N bitcoin transactions, where N is equal to the number of users, in our case, 3. Each user gets a copy of these transactions, with each one defining a “round” (e.g. round 1, round 2…round n).
The transaction defining round 1 has a number of outputs equal to 3 + N. (See Figure 3.) The first output puts 240 sats in an anchor address, which, via child-pays-for-parent, will be used to pay the mining fees for the round 1 transaction. The second output puts 100,000 + 240 sats in a “midstate” address to be described momentarily. The third output puts the remainder back in the multisig, ready for use in the next round, minus an amount of sats equal to 294 * N. These sats get divided into N connector outputs with a value of 294 sats apiece. The function of these connector outputs will be described after two more paragraphs.

Figure 3.
The transactions defining every subsequent round only have 3 outputs apiece (see Figure 4); these are identical to the first three outputs of the first round, except the third returns a smaller remainder to the multisig each time, until, in the last round, there is no third output because there’s nothing to return to the multisig.

Figure 4.
In each round, the person wishing to withdraw in that round broadcasts the transaction defining that round and pays its fee using the anchor output created in its first output and attaching a fee via child-pays-for-parent. However, the money they wish to withdraw is not yet in the withdrawer’s channel. It is in a midstate address, i.e. an address used when the user is in a state between initiating a withdrawal and finally withdrawing.
The midstate address has N script paths, each of which lets a different user spend that utxo, but only with N-of-N signatures, i.e. a signature from every other party; these signatures are generated during the signing ceremony and shared with everyone. These signatures each require two inputs: the midstate address itself and one of the connectors. This is why the number of connectors is equal to the number of users: each one “gets” one, and in each round, they can only withdraw by consuming the connector that is pertinent to them (see Figure 5). Consuming that connector ensures the user cannot withdraw in a subsequent round (see Figure 6); their connector is gone, so the signatures which would have allowed them to withdraw in that round are invalid, because they commit to that connector as a second input, and bitcoin prevents it from being spent twice.
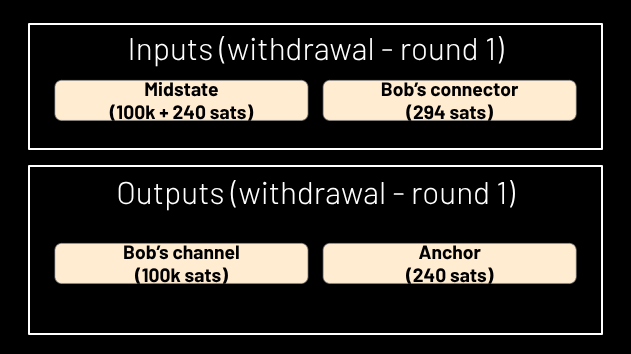
Figure 5.
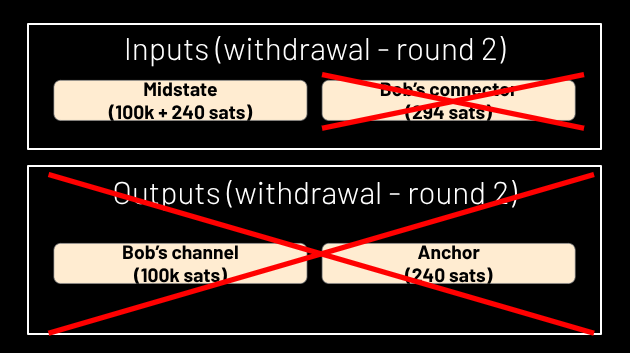
Figure 6.
In this document, these outputs are called “connectors” because they “connect” the signatures allowing for a unilateral withdrawal to bitcoin's consensus rule forbidding doublespending, and thus this consensus rule prevents any user from withdrawing from the coinpool twice.
Thanks to the existence of the connector, a user can only withdraw from a single midstate address, but they can withdraw from “any” of them, i.e. in any round. In order to withdraw, the user must supply the N-of-N signatures for their script path in the midstate and consume their connector. The N-of-N sigs also force the user to create two outputs from the midstate: one puts 240 sats in an anchor address – which the user must use to pay the fee for withdrawing from the midstate, via child-pays-for-parent – and the other puts 100,000 sats in the user’s channel.
A coinpool that uses the exit ladder mechanism has a problem. All the money therein starts out in an N-of-N multisig, and in every round, it returns to the N-of-N multisig. But, when used with payment channels, as I use them in this protocol, this creates a problem if multiple users become unresponsive.
Before I outline the problem, let me share how users are supposed to exit the coinpool in the “happy path.” Each user’s money is in a payment channel, and I will outline later how they can use their channel to receive money and send it to other people on the lightning network, or on the base layer. The “happy path” exit starts with that: the user sends out their entire balance to a lightning wallet or a base layer wallet.
Once they’ve done this, they can tell the admin that they are done using the coinpool, and disclose to him their private key. If every user does this (Alice, Bob, and Carol in our example), then Reginald ends up with all 4 private keys in the 4-of-4 multisig. So he can sweep all funds out of it, and thus terminate that particular coinpool permanently. In this case, the exit ladder never gets used.
Now let us suppose Alice, Bob, and Carol have been using the coinpool for several years, and they each have significant balances. Alice leaves via this “happy path,” but Bob and Carol do not. If Reginald wants to stop serving this coinpool, he can, of course, just stop doing so, and then Bob and Carol can do nothing but exit via the exit ladder – or via the happy path, if he is willing to provide the minimal service of helping them exit efficiently. But what if they take a very long time to do so, or never do so? Reginald has some money in their channels but it’s inaccessible to him unless they exit. He might broadcast their exit transactions “for them” and pay the exit fees himself, but if lots of users disappeared, this could be very expensive. So users of a coinpool can effectively “hold Reginald’s money hostage” and make him pay a large amount in mining fees to recover it. That’s a problem.
To fix this problem, each round of the exit ladder should have one additional transaction that everyone signs. This transaction lets Reginald take all the money left in the multisig in that round, but the signatures consume two inputs: the multisig itself, and another output – which I call the “countdown output” for reasons to be disclosed in the following paragraph – that Reginald may create at any time (see Figure 7). Moreover, these signatures use the sequence field to ensure that they are only valid if the countdown output has existed for 1 month and the multisig output has existed for 1 week.

Figure 7.
With these signatures in hand, Reginald no longer has to worry about users becoming unresponsive or making him pay a large amount in mining fees to recover his money. He can just create the countdown output, and that effectively initiates a 1 month countdown. Once that countdown is up, Reginald can take all of the money left in the multisig. The users, until then, can all still exit using their presigned transactions, or via the “happy path.” And each time one of them exits, if the month is already up or about to be up, that exiter effectively adds an additional week to the countdown, which means all of the users have plenty of time to exit. This fixes the problem. Users cannot hold Reginald's funds hostage for longer than 1 month plus N weeks, nor make him kick out every unresponsive person individually and thus pay a large amount in mining fees to recover his share of each channel.
The exit ladder requires two transaction packages containing two transactions apiece. The first package contains a transaction that creates the midstate and a second that pays mining fees; the second package contains a transaction that moves 100,000 sats from the midstate into a channel and a second that pays mining fees. The division of the exit protocol into two transaction packages creates an opportunity for a race condition.
Suppose Alice and Bob both decide they want to exit the coinpool via the exit ladder in the same round. One of them will be the first one to broadcast and pay for the first transaction package – let’s suppose it’s Alice. As soon as Bob sees this package enter the mempool, he can rejoice: Alice already paid the mining fee for the first transaction package, but all that does is put the money in the midstate. Bob, like Alice, has not yet exited the coinpool, so he has not yet consumed his connector, meaning he can withdraw from the midstate just as well as Alice can. So Bob can now enter a race with Alice: who will get to withdraw from the midstate first? (See Figure 8.)
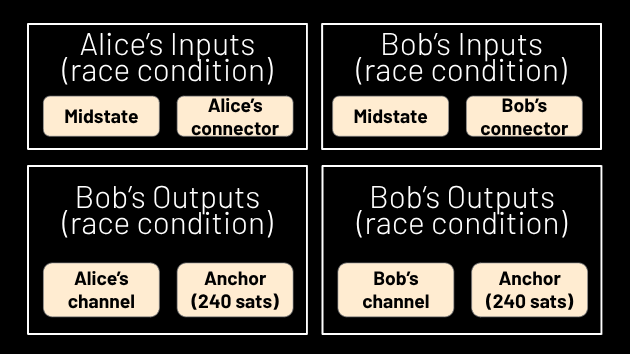
Figure 8.
Both of their transactions attempting to do so are valid, since neither one has consumed their connector yet, so miners pick the winner. If Bob wins, Alice lost money by paying for the first transaction package, and she will have to do so again and hope that this time, there will be no race condition, or if there is one, she wins it. Note that her ability to exit from any midstate is unaffected by losing a race condition; if she loses the race, that means her connector has not been spent yet, so she can leave in a future round, but still, it sucks that anyone can unfairly lose money just because someone else initiated a race condition.
I wonder if game theory makes race conditions of this kind unlikely, for the following reason: presumably, Bob would only enter this race condition in order to save money on fees by not paying for the first transaction package. But Bob has no greater chance of winning the race than Alice unless he pays extra fees to "bribe" miners to favor his transaction. And if he pays extra fees, they may well push his total cost higher than if he just waited for the next round and paid for the whole thing at standard fee rates. So I doubt there is much incentive for Bob to do this. But anyway, it would be nice to have a cryptographic solution to this problem rather than hoping game theory fixes it.
It is also worth noting that it seems unlikely that users will ever encounter the race condition described above because the use of the exit ladder is only a fallback anyway; users are normally expected to exit via the “happy path” where they send their money out of the coinpool using Reginald as a bridge. The exit ladder is only there in case Reginald stops serving some user, so the race condition only applies if he stops serving two users who both decide to unilaterally exit in the same roughly-20-minute period (20 minutes because the first user must first put the first package in the mempool and wait for it to be mined, which takes about 10 minutes, then the race to withdraw from the midstate can begin and the winner is discovered when the block after that is mined – which takes another 10 minutes, roughly).
When a user exits the coinpool, their money (100,000 sats) goes into a payment channel. The user and Reginald both know, in advance, that the txid and vout of this channel will be one of N possibilities, depending on which round the user exits in. The user and Reginald also know the amount that will go into this channel (it will be 100,000 sats) and they know the channel’s address. By knowing the txid, vout, amount, and address in advance, Reginald and the user can create an initial state within this payment channel and update that state. (Those four items are the main variables you need to know in order to create a presigned transaction.)
The channel starts out with all of its funds on Reginald’s side, but if Reginald wishes to send money to the user, he and the user can cosign N state updates, each of which affects one of the potential channels the user will end up with depending on which round he exits in. (See Figure 9.) All N state updates push the same amount of money to the user’s side of a potential channel, so as long as the user validates all N state updates, he knows he will definitely receive that amount in the channel he eventually exits with, no matter which round he exits in.

Figure 9.
The ability to update a payment channel’s state allows the user to receive money from Reginald. The user starts out with no money on his side of the channel, so all he can do with that channel is receive money from Reginald. But he can also receive money from other bitcoin users, as long as Reginald serves as a bridge.
To illustrate, imagine a bitcoin user “not” in the coinpool – Dave – wants to send 5,000 sats to Alice, who is in the coinpool. Alice can make up a 32 byte secret and run it through a sha256 hash function to get its hash. Now Alice works with Reginald to create a “base layer” bitcoin address, encoding a contract that says this: Alice can take the money in this address after 2 weeks or Reginald can take it if he learns (and discloses) the secret which, currently, only Alice knows.
Alice shows this bitcoin address to Dave, who sends 5,000 sats into it. Then Alice works with Reginald to create a state update in her channel: instead of having all of it on Reginald’s side, 5,000 sats will move from Reginald’s side into an off-chain HTLC output, such that Alice can take the money if she discloses her secret, otherwise Reginald gets the money after 2 weeks minus 1 day.
And now we do an off-chain swap: Alice gives Reginald her secret, and they “resolve” the off-chain HTLC via a new state update, such that Alice now has 5,000 sats on her side of the channel and Reginald has the remainder on his. With the secret in hand, Reginald sweeps the funds from the on-chain HTLC, thus resolving that, too.
Voila, Alice received money from a user of bitcoin’s base layer, in such a way that her balance in the coinpool grew from 0 to 5,000 sats. Reginald, meanwhile, “lost” 5,000 sats from “his” side of the channel, but it’s okay because he got compensation: he received 5,000 sats from Dave. (See Figure 10.)
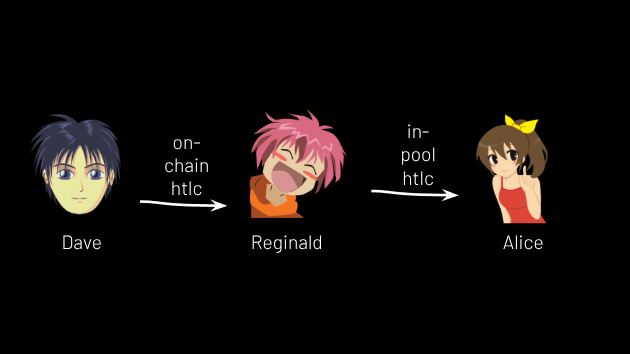
Figure 10.
Alice can use a similar trick to receive money from lightning users. Suppose a lightning user Edna wants to send 6,000 sats to Alice via lightning. Alice can again make up a 32 byte secret and get its hash. She gives its hash to Reginald, who uses his lightning node to create a lightning invoice that he can only settle if he learns Alice’s secret. He shows this invoice to Alice, who shows it to Edna. Edna pays it, but Reginald cannot settle it, due to not knowing Alice’s secret. But then we do a swap again: Reginald creates an HTLC in Alice’s channel whereby she can take 6,000 sats if she discloses the secret. She does so, whereupon she and Reginald resolve the “in-coinpool” HTLC, and Reginald uses the secret to resolve the lightning invoice. Voila, Reginald “lost” 6,000 sats from his side of the channel, but got compensated with 6,000 sats on lightning; Alice effectively received 6,000 sats from Edna, and her coinpool balance went up from 5,000 sats to 11,000 sats. (See Figure 11.)
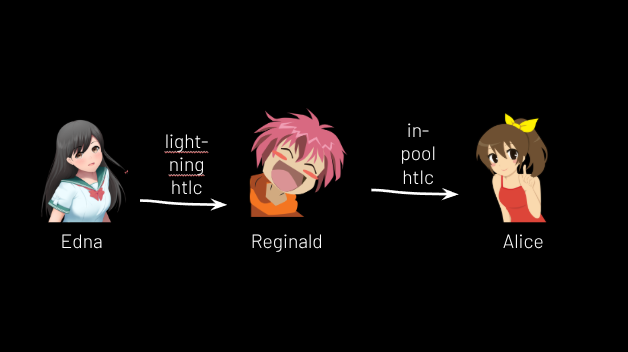
Figure 11.
Alice can use the reverse of the above process to send money to people outside the coinpool. Suppose she wants to send Dave 5,600 sats. Reginald can make up a 32 byte secret, hash it, and create a bitcoin address encoding the following script: Reginald gets the money after 2 weeks, otherwise Alice can take the money if she learns (and discloses) the secret. Reginald funds this address with 5,600 sats. Now, Alice creates an HTLC worth 5,600 sats in her channel with Reginald, such that Reginald can take the money if he discloses the secret. He does so, and they resolve the “in-coinpool” HTLC, meaning Reginald gained 5,600 sats in the coinpool. Now, with the secret in hand, Alice uses it to create a transaction on bitcoin’s base layer sweeping the money from the “on-chain” address and sending it to Dave. Alice’s coinpool balance is now 5,400 sats (11,000 - 5,600 = 5,400). (See Figure 12.)
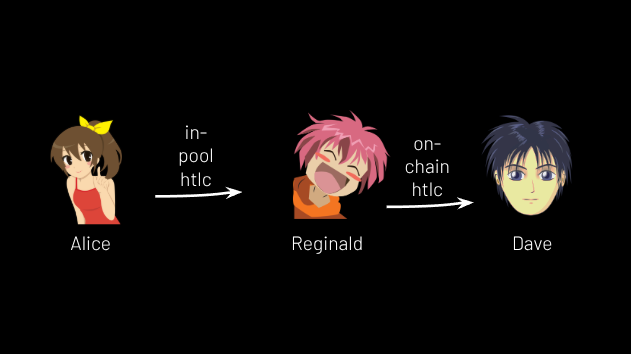
Figure 12.
If Alice wants to pay 5,400 sats to Edna via lightning, she can get a lighting invoice from Edna worth 5,400 sats, extract its payment hash, and create an HTLC worth 5,400 sats in her channel with Reginald. Reginald can take the money if he learns (and discloses) the preimage to Edna’s hash, which he learns by paying Edna’s invoice, whereupon he shares it with Alice. They resolve the “in-coinpool” HTLC, meaning Reginald gained 5,400 sats in the coinpool (but lost it on LN by sending it to Edna) and Alice’s balance is now 0. (See Figure 13.)
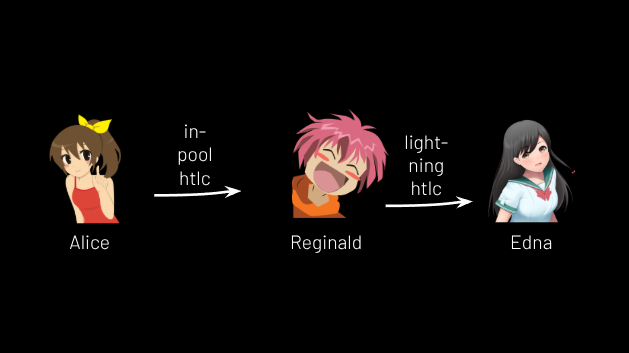
Figure 13.
Each user of every coinpool has a payment channel that can send and receive via lightning, as described above. Therefore, they can pay one another via lightning payments. Just as Alice could send money to Edna, a lightning user, she can send money to Bob or Carol, who are in her coinpool, by just doing the same thing she did for Edna. Bob and Carol act like Alice acted when she wanted to receive money from Edna, except this time they are receiving it from Alice. Reginald acts as a lightning routing node, routing payments between users of any coinpool he serves, or to users of coinpools served by people other than Reginald. (See Figure 14.)
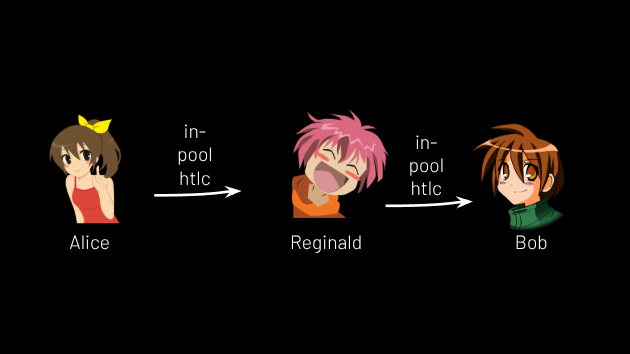
Figure 14.
The above protocol works fine with lightning, but there is an alternative type of payment channel that is even better suited for this context, called a hedgehog channel. Hedgehog channels are very similar to lightning channels, but they allow for asynchronous payments, which unlock many new features, such as automatic subscription payments.
Hedgehog channels work like this: suppose Alice and Reginald want to create an initial state where all of the funds are on Reginald’s side. Alice needs to know Reginald’s pubkey and the hash of a secret that only Reginald knows. She already knows his pubkey because it’s the one he gave her earlier when they set up the coinpool multisig, so she only needs to ask him for the hash. With these two piece of data in hand, she creates a transaction putting all of the channel funds in a “pending state” (see Figure 15) encoded in a bitcoin address with a script containing the following logic:
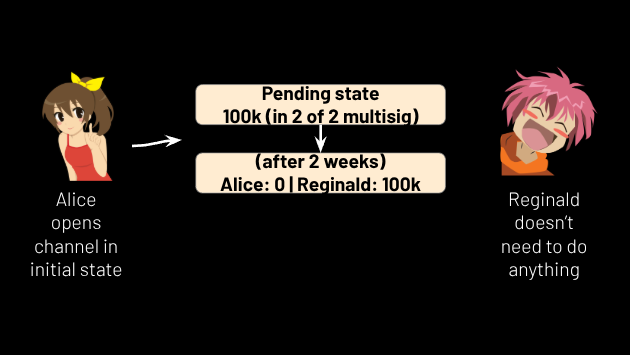
Figure 15.
Using branch one, Alice now creates a second transaction that takes all of the money from this pending state and sends it to Reginald. Having created these two transactions, Alice signs them, but her signature on the second transaction commits to a relative timelock of 2 weeks. She gives both signatures to Reginald, along with the hash of a secret which “she” creates and whose purpose will be described in section 14. If Reginald cosigns the transactions given to him by Alice, he can broadcast them and thus get all of the money out of the channel, after a 2 week delay. Voila, the initial channel state is created: all of the funds are on Reginald’s side of the channel.
Now let us suppose Reginald wants to send 7,000 sats to Alice. He needs to know Alice’s pubkey, which he already knows because it’s the one she gave him earlier when they set up the coinpool multisig, and the hash of her secret, which he already knows because she sent it to him in the previous paragraph. So now Reginald creates a transaction putting all of the channel funds in a new pending state (see Figure 16) with the following logic:
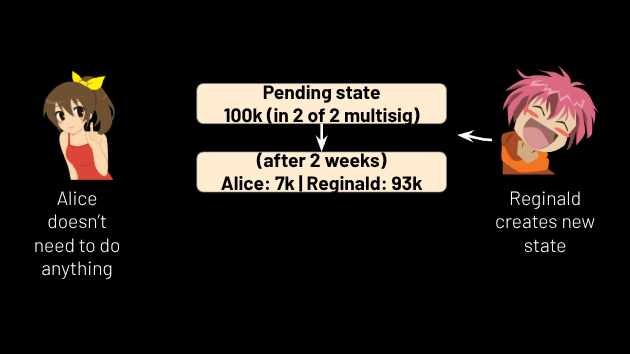
Figure 16.
Using branch one, Reginald now creates a second transaction that takes all of the money from this pending state and disperses it like this: Alice gets 7,000 sats and Reginald gets the other 93,000 sats. Having created these two transactions, Reginald signs them, but his signature on the second transaction commits to a relative timelock of 2 weeks. He gives both signatures to Alice, along with the hash of a new secret. If Alice cosigns the transactions given to her by Reginald, she can broadcast them and thus get 7,000 sats out of the channel, after a 2 week delay.
Alice and Reginald can keep doing this procedure indefinitely, sending one another a new hash each time and distributing the funds according to the new state.
In section 13, I promised to describe the purpose of the secrets Alice and Reginald keep creating. These secrets assist with a penalty mechanism that disincentivizes Alice or Reginald from broadcasting an old state. This penalty mechanism works in a manner similar to the one used in lightning, but it is modified to be more flexible and only penalize sometimes. Before I describe how it works, I want to say why I modify lightning’s penalty mechanism.
Hedgehog is designed so that the sender can create a state update without waiting for the receiver to “do” anything. If Reginald wants to send Alice 10,000 sats, he creates a state where she has that many more sats than she had before, signs it, and sends the data to Alice, without waiting to receive anything back from her. However, this design brings a problem: what if Alice disappeared? What if she never signs Reginald’s state update? Since either party might disappear and never confirm the latest state, I need a way for either party to close the channel even if the latest state never gets signed by both parties. So I allow either party to initiate a channel closure in the most recent “prior” state.
So suppose the current state is state 2, where Reginald has 93,000 sats and Alice has 7,000 sats. Reginald sends Alice 10,000 sats in a new state update, state 3, so that Reginald’s new balance is 83,000 sats and Alice’s is 17,000 sats. A month goes by with no interaction between them, and Reginald wants his 83,000 sats back, but does not want to terminate the whole coinpool, because he is still making money from routing payments from the other users. So, he broadcasts the “exit” transactions necessary to get his channel with Alice on the blockchain without affecting the other coinpool users.
Then he broadcasts a transaction initiating a channel closure by putting the funds in the pending state, but this pending state does not correspond to the “latest” state, because Alice never sent him signatures for the latest state. So if the 2 weeks go by without Alice acting, the state that will confirm on the blockchain is the state where Alice had 7,000 sats instead of 17,000 sats, because that is the most recent state that Reginald had signatures for. That’s no good for Alice! If this was a lightning channel, Reginald would have sent Alice a revocation key when updating the state, after receiving a revocation key from her and a set of signatures cosigning the new state. Then, Reginald would not have to broadcast an old state, and if either of them tried, they could use their counterparty's revocation key to penalize the would-be-cheater by taking all of their money.
But I don’t like that model because it requires both counterparties to cosign every state transition before either one considers it final, which makes asynchronous payments harder. What I do instead is this: when Reginald sends Alice the signatures for the latest state (the one where she has 17,000 sats), he also sends her a signature for a transaction that takes as an input the most recent “prior” state’s pending state (the one where Alice had 7,000 sats), and distributes the funds according to the latest state (the one where Alice has 17,000 sats). That way, if Reginald broadcasts the most recent prior state, Alice can fix it by broadcasting a transaction that “updates” it to the latest state with no penalty (see Figure 17). This allows either party to consider each state update final without waiting for their counterparty to get online. The sender can still broadcast the most recent prior state, but if they do, the recipient is incentivized to “correct” it to the latest state, and they have two weeks to do so.
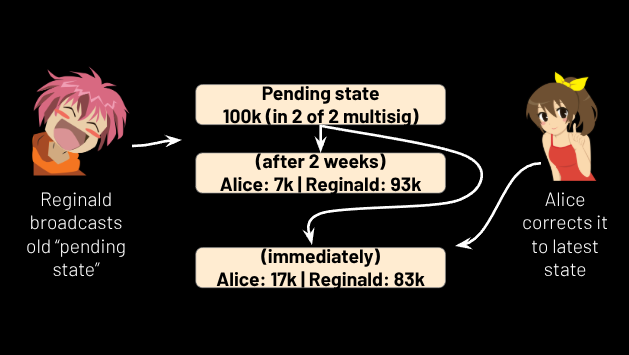
Figure 17.
And this is where the secrets come in: to prevent too many prior states from being valid, the next time Reginald sends money to Alice, he also sends along the secret to the pending state two states ago that paid him money. This means it is unsafe for him to broadcast a pending state other than the latest state or the most recent prior state; if he broadcasts any state from before that, Alice can use the secret he disclosed to sweep all funds from the pending state via branch 2. (See Figure 18.) Symmetrically, whenever Alice sends money to Reginald, she also sends along the secret to the pending state two states ago that paid her money. Thus neither party can broadcast “too old” of a state; they can only broadcast the latest state or the most recent prior state, which, if they do the latter, their counterparty can correct it to the latest state with no penalty.
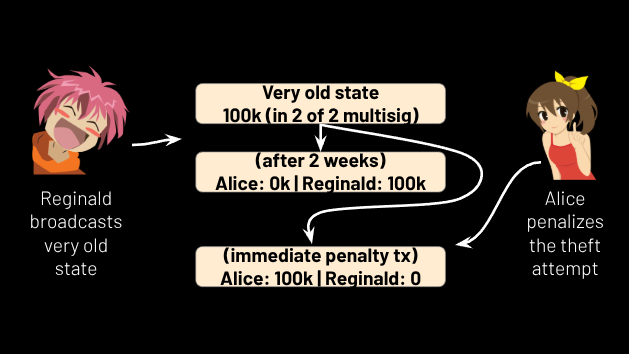
Figure 18.
Hedgehog allows the sender to consider a state update final without waiting for their counterparty to respond. That is a big difference between hedgehog channels and lightning channels. Another is this: a hedgehog channel only uses relative timelocks in state updates, whereas the lightning network uses some absolute timelocks, e.g. for HTLCs. Relative timelocks are better for asynchronous payments because the “timer” doesn’t start counting unless something goes so wrong that one of the channel users decides to force close. This allows for a long amount of time to go by before an HTLC has to be resolved, which allows for Reginald to be very patient when waiting for a user to settle a pending asynchronous payment.
The disuse of the absolute timelock field also allows it to be repurposed. For example, suppose Reginald charges a monthly fee of 1,000 sats to be in his coinpool, and if it goes unpaid, he kicks you out. Since hedgehog payments don’t use the absolute timelock field in the same way lightning does, Alice can create a transaction that pays 1,000 sats to Reginald, but sign it with a signature that commits to an absolute timelock set for 1 month in the future. She can also create another one with an absolute timelock 2 months in the future, and another one set for 3 months in the future.
She can give all three signatures to Reginald, and as the months tick by, one by one, Reginald can claim these “subscription” payments, even if Alice doesn’t get online again. (See Figure 19.) This allows Alice to subscribe to Reginald’s coinpool without giving up custody of her funds til the signatures become valid, and without needing to come online again when the bill comes due. She can also cancel her subscription at any time by simply exiting the coinpool.
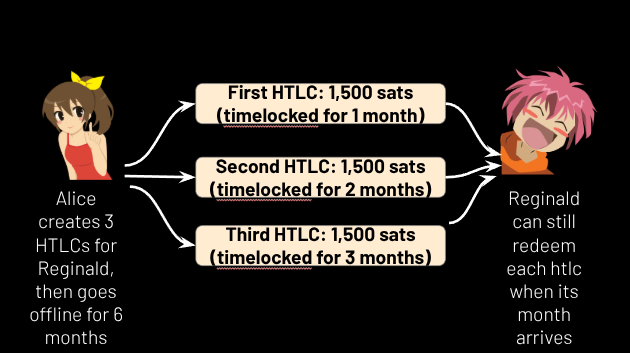
Figure 19.
A similar trick allows Alice to subscribe to third party services not provided by Reginald. If she wants a 12-month subscription to “Bitflix,” a streaming media platform that charges 1,500 sats per month, she can create 12 HTLCs in her channel with Reginald, each worth 1,500 sats, and each locked to a different preimage that only Alice knows. She can use the absolute timelock field on these HTLCs to make each of them claimable by Reginald at the beginning of a different month in the future, but only if he learns the corresponding preimage.
Alice can then send her preimages to Bitflix and inform them that Reginald wants these preimages; each one is worth 1,500 sats to him, so he will be happy to pay a 1,500 sat lightning invoice each month if it is locked to the same preimage that allows him to claim the 1,500 sat HTLC for that month. Bitflix can then contact Reginald once per month, even if Alice is offline, and “sell” him the preimage for that month for 1,500 sats. Thus Alice can subscribe to a third party service and Reginald can auto-deduct an approved amount of funds from her coinpool balance for that service without Alice losing custody of her funds until the pre-approved moment of redemption.
The same trick also allows for asynchronous payments from Alice to anyone. She can create an HTLC in her channel with Reginald worth whatever amount she wants to pay someone, locked to a preimage that only she knows, and then send the preimage to whoever she wants to pay, informing them at the same time that Reginald wants that preimage so much that he will pay a lightning invoice for it as long as it is valued at the same amount as the HTLC she created. Even if Alice goes offline now, the third party can sell that preimage to Reginald for the value Alice told them, whereupon Reginald can claim the HTLC in Alice’s channel, even if she is still offline. This effectively allows Alice to asynchronously pay anyone on the lightning network or in a coinpool that supports this feature.
This document began with a goal: allow Reginald to create coinpools for people and serve them as a bridge node, routing payments not just within the coinpool, but to the wider bitcoin network. I think I have shown that he can do this using the bridging protocol outlined in sections 11—12, and earn money not just from routing fees but also by charging a monthly fee to the users of his coinpools via the subscriptions feature described in section 15.
I had a goal of allowing the users of Reginald’s coinpools to exit them unilaterally, if necessary, such that Reginald never has custody of anyone’s coins. I think I have shown that they can do this using the exit ladder described in sections 6—8, meaning this protocol also counts as a new layer 2 for bitcoin.
I had a goal of giving each user a payment channel which they can use to send payments within the coinpool for free and to the wider bitcoin network for a fee. I think I have shown that they can do this using the hedgehog channels described in section 13, and that these bring in awesome new features like asynchronicity and subscription payments, as described in section 15.
I had a goal of ensuring that each coinpool should exist independently of all the others and last an indefinite period of time, until all of its users exit. I think I have shown that this is feasible using the multisig described in section 3, though due to the countdown mechanism discussed in section 7 as well as the fact that Reginald can just stop serving a coinpool at any time, it is sometimes possible that some users might desire to exit a coinpool sooner than they might have otherwise hoped.
I think these characteristics make this coinpool model a good fit for general use in bitcoin. I hope that good coders will implement these ideas and that the next generation of bitcoin wallets will allow users to benefit from the features described. Let’s work together to keep bitcoin the best money in the world.